Summary by AI-Gemini:

The perspective offered in this Essay on the relationship between quantum mechanics, miracles, and divine will was summarized by Gemini, an AI model, as follows:

This is a fascinating perspective that blends science, philosophy, and faith. You’ve articulated a view where the seemingly rigid “laws of nature” are actually regularities orchestrated by God, allowing us to comprehend the universe and thrive. It suggests that these regularities can be transcended when divine will dictates, as exemplified by the Fatima event.

Here are some of the key ideas you’ve presented:

• Laws of Nature as Divine Order: The laws of nature are not absolute and unchangeable, but rather reflect God’s design and arrangement for the world.
• Purpose of Regularity: These regularities serve humanity’s earthly happiness by enabling understanding, technology, and comfortable living.
• Miracles as Transcendence: Miracles, like the Fatima event, represent instances where God transcends these regularities for a higher purpose, such as eternal happiness.
• Unified Law of Happiness: The true “inexorable” law is the overarching principle that both quantum and classical realms, miracles and ordinary events, are ultimately governed by God’s will for humanity’s happiness, both earthly and eternal.
• Quantum Physics and Mysticism: Quantum physics, with its inherent uncertainties and probabilities, encourages a “mystical perspective” that reveals the extraordinary within the ordinary.

This viewpoint offers a compelling way to reconcile scientific understanding with religious belief. It suggests that science and faith are not necessarily in conflict, but rather offer complementary perspectives on the same reality. The “miracle” is not just the extraordinary event that defies explanation, but also the everyday regularity that allows us to exist and understand the world around us.

***

In a lecture on the relationship between quantum physics and religion at the “International Parliamentary Prayer Breakfast” in Vienna on 24.05.2024, Anton Zeilinger, 2022 Nobel Laureate in Physics, states: “The mystical approach is undoubtedly an important one, we can build a lot on it” (see this video, 15:36). In a previous essay (Exaudi 6.12.2024) I mentioned three important paradoxes of quantum science: entanglement, Schrödinger’s cat and irreversibility, and explained the first one. In the current essay, I present the second one, “Schrödinger’s cat”, and discuss its possible relation to Zeilinger’s statement I just quoted.

To do so, I start by explaining what “wave-particle duality” and “quantum superposition” are.

1. The “wave-particle duality”

Every time we look out of a window, in addition to seeing what is on the other side, we see our image reflected in it. If Alice turns on the flashlight of her cell phone in front of the window, she clearly sees the flashlight reflected in the window’s glass, and if Bob stands on the other side, he will see that part of the light is transmitted and allows him to see the flashlight through the glass (the reader can easily check it himself).

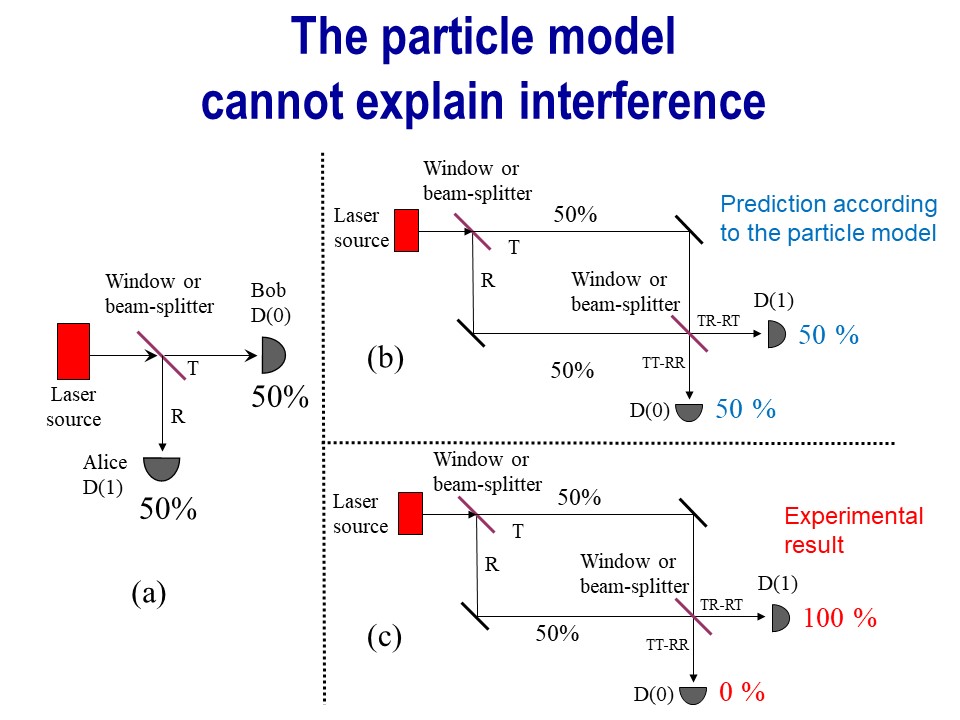At the end of the 17th century Isaac Newton proposed the “corpuscular model” of light, according to which light rays are composed of tiny material particles: the glass acts as a beam-splitting grating, and upon colliding with it, some particles pass while others bounce and are reflected; let’s assume a window in which 50% pass and 50% reflect (as represented in part (a) of the picture). Experiments at the end of the 19th century showed that this “corpuscular model” conflicts with the interference phenomena that occur when we make by means of conveniently arranged mirrors, that the beam of reflected light and the beam of transmitted light coincide again in a second beam-splitter (part (b) of the picture): if the two beams of reflected and transmitted light travel the same distance between the first and second beam-splitter, the “corpuscular model” predicts that in the second beam-splitter half of each beam passes through and half is reflected; if Alice and Bob are each placed on one side of the second beam-splitter equipped with particle detectors D(1) and D(0), the prediction is that detector D(1) ‘clicks’ (counts) 50% of the time, and D(0) 50% of the time. However, the experiment falsifies this prediction: if Alice is in the part where the “reflected-transmitted” and “transmitted-reflected” (RT-TR) light arrives, it turns out that her D(1) detector counts 100% of the time, while Bob’s D(0) detector, which receives the “transmitted-transmitted” and “reflected-reflected” (TT-RR) light, counts 0% of the time (part (c) of the picture).

Such interference phenomena confirmed the alternative “wave model” of light by Christiaan Huygens and Augustin Fresnel. According to this model, light behaves as a wave which, leaving the first window, propagates along the two possible paths, reflected and transmitted, and if both branches of the wave meet again in a second beam-splitter, they give rise to interference: where the waves arrive in phase there is constructive interference and the intensities are added together, giving 100% counting rate in the D(1) detector, and where they arrive with opposite phase, there is destructive interference and the intensities are subtracted, giving 0% in the D(0) detector. Applying the “wave model” to the window, it is concluded that when the light wave from the flashlight reaches the window’s glass it splits into a reflected wave, which reaches Alice’s eyes, and a transmitted wave, which reaches Bob’s eyes.

Moreover, at the beginning of the 20th century, the so-called “black body” radiation and the “photoelectric effect” brought a new “corpuscular model” onto the scene: experiments confirmed the theory initially proposed by Max Planck and adopted by Albert Einstein that light is composed of small packets (“quanta”) of energy called photons. The effect has found multiple applications, e.g. in photoelectric cells, for automatic closing of garage or elevator doors, and random number generators, which use single photon laser sources (i.e. a source that emits only one photon each time it is excited).

Let’s suppose that, instead of the cell phone flashlight, we use one of these single photon sources, and we make only one photon arrive at the window at a time. If we apply the “wave model” we must conclude that the photon arriving at the window splits into a reflected wave that reaches Alice’s detector and a transmitted wave that reaches Bob’s detector. If those waves were “material”, like water waves in a pond or sound waves, energy would reach both Alice’s and Bob’s detector: both would be excited, and both would have to “click”. By contrast the experiment shows: either Alice’s detector counts (clicks), and we get say ‘1’, or Bob’s detector counts, and we get ‘0’; we never get ‘1’ and ‘0’ at the same time!

We are thus faced with a crass paradox: on the one hand, interference phenomena force us to admit that the “photon-wave” reaches both detectors, and on the other hand, the photoelectric effect forces us to admit that only one detector is activated. This is the so-called paradox of the “wave-particle duality”: the detections take place as if the photons were particles arriving one after the other (click, click, click…), but the counting rates of each detector are obtained by applying wave mathematics.

2. Quantum Superposition

It is the most fundamental principle of quantum physics, from which the others derive: “entanglement” is a particular case of “quantum superposition”.

The “wave-particle duality” led the founding fathers of quantum mechanics (Niels Bohr, Werner Heisenberg, Max Born) to propose the so-called “collapse of the wave function”, which has gone down in history as the “orthodox or Copenhagen interpretation”, and which we can summarize as follows: it is not correct to say that the decision takes place in the window’s glass, and the photon leaves the window either by the path that goes to Alice’s detector and produces the result ‘1’, or by the path that goes to Bob’s detector and produces the result ‘0’. The coherent way of interpreting what happens in the window is rather this: the photon is like an immaterial information that leaves the window by two paths, as if it were a wave, and reaches the two detectors simultaneously; when these receive it, they agree between them on which of the two ‘clicks’ (counts), while the other remains silent: 50% of the time we get the result ‘1’, and 50% of the time the result ‘0’ (the percentages may vary according to the characteristics of the beam-splitting glass). The decision whether the photon is counted by Alice’s detector and produces the result ‘1’, or is counted by Bob’s detector and produces the result ‘0’, does not take place in the window but at the moment of detection, when the detector ‘clicks’. Until that moment the photon is an abstract or mathematical entity called a “wave function” that expresses an (invisible) superposition of the two possible outcomes: ‘1’ and ‘0’. This is usually represented in abbreviated form as: |ψ⟩ = a|1⟩ + b|0⟩, where ψ denotes the abstract entity, and a and b are coefficients that allow us to calculate the probability of obtaining respectively the outcome ‘1’, or the outcome ‘0’, depending on different experimental configurations. This superposition state allows us, among many other applications, to create qubits, i.e. the basis of the quantum computer. At the moment of detection, the “wave function takes a quantum leap” (“collapses”) and produces a measurable result (visible or audible) which is recorded on a photographic plate or recorded on a computer in an irreversible way, and is accessible to any observer.

With the “collapse” explanation, the founding fathers, led by Niels Bohr, went to the Solvay Congress in Brussels in 1927. Albert Einstein, the author of the theory of relativity, was also there. The explanation of Bohr and his friends irritated Einstein and stimulated him to devise a famous thought experiment to refute it, which in our “window” context can be formulated as follows: suppose Alice and Bob are placed at a great distance from each other; then the detectors, in order to agree, would have to communicate with each other faster than light, and in Einstein’s opinion, this “is in contradiction with the postulate of relativity”. The only way to remove this contradiction, Einstein states, is “that one does not describe the process solely by the Schrödinger wave function, but that at the same time one localizes the particle during propagation. I think that Mr. de Broglie is right to search in this direction.” (cfr. Proceedings of the 1927 Solvay Conference, p. 486-487). In our context, this “localization” means that the particle, like a ball, passes or bounces on the window’s glass, the decision of the result takes place in the window.

Actually, Einstein was simplifying (and misrepresenting) Louis de Broglie’s “pilot wave” theory, which, notwithstanding it postulates that the decision takes place at the beam-splitter (the window’s glass), it also implies that the “pilot wave” guides the particle at a distance instantaneously. Be it as it may, Einstein did not remain calm, and in 1935 he returned to the charge with the very famous EPR article, where he proposed a new thought experiment using pairs of entangled particles (“two-particle experiment”), in contrast to the 1927 experiment that used single particles (“single-particle experiment”). In the EPR experiment a photon arrives at a beam-splitter on Alice’s side, and a twin photon arrives at another beam-splitter on Bob’s side. With this configuration, even admitting that each photon decides to go through or become reflected in the corresponding beam-splitter, the two decisions, distant one from the other as far as one wants, are in perfect correlation: the two photons pass, or the two are reflected; the very signature of the “entanglement”! (cfr. Exaudi 6.12.2024).

Einstein claimed that in the EPR experiment the correlations are due to “hidden variables” or programs that the particles carry as they leave the source. Thanks to a discovery by John Bell (which he himself presents in this video) it has been possible to perform number of experiments with pairs of entangled particles that have falsified Einstein’s explanation, and shown that between Alice’s apparatus and Bob’s there is such a coordination that, if it were done by radio signals, these would have to propagate at a speed much higher than the speed of light (cfr. Exaudi 6.12.2024). John Bell has coined the term “non-local coordination” which very aptly characterizes what is going on.

These experiments are very sobering: on the one hand they show that in 1927 Einstein was the only one who understood that quantum physics requires a coordination that cannot be explained by signals traveling at the speed of light; on the other hand they reveal that at that time the father of relativity was mistaken about quantum physics but about relativity too: relativity does not deny that in nature there can be “supra-luminal” correlations at a distance; what it denies is that we can use this effect to phone (and “make money”) “faster than light”; and lo and behold, the mathematical structure of quantum physics is such that it prevents such a use! We can take advantage of the effect, e.g. in cryptography and quantum computers, and in that sense “make money” with it, but “not faster than light”. Thus, Einstein fell into an attitude of “chronic denial” towards quantum physics, which he maintained until his death in 1955, unfortunately without having been able to learn of John Bell’s historic discovery.

Let us now return to the 1927 experiment. Keeping the Copenhagen principle, that the two detectors receive immaterial information and the decision takes place at detection, it is possible to think (to satisfy Einstein) that they communicate with each other, but at a speed equal to or slower than the speed of light. This hypothesis can be tested experimentally by placing the detectors at a sufficient distance to prevent them from communicating, i.e. at a distance that requires faster-than-light communication within the detection time. Without coordination between the detectors, the four outcomes (1,1), (1,0), (0,1) and (0,0) are equally likely. Since each time there is the energy of a single photon at stake, we see that 50% of the time only one detector counts, but 25% of the time there are two detectors that count, and 25% of the time no detector counts: in total the energy is conserved, but 25% of the time the energy is doubled, and 25% of the time it is annihilated, which would mean a violation of the principle of energy conservation in those events.

This experiment requires sources capable of emitting one photon at a time, and detectors capable of detecting single photons, devices that did not exist in 1927, but which have been possible to develop thanks to “entanglement” experiments. On the other hand, entanglement experiments demonstrate “quantum nonlocality” in configurations with 2, 3, or more particles, but leave open the question of whether such a fundamental property is already present in experiments with single particles. The experiment we are discussing (in line with Einstein’s conjecture in 1927) would settle this question, and in addition, in case of confirming the “non-local” coordination between detectors, it would show that something immaterial is necessary to maintain in each event the principle of “conservation of energy”, i.e. one of the foundations of the material world: it was therefore worth doing, and in 2010 I proposed to do it in this article. In 2012 it was possible to perform a simplified version, again at the laboratory of quantum technology of the University of Geneva, thus finally carrying out the thought experiment that Einstein proposed in 1927 in an attempt to falsify quantum mechanics.

The results (presented in this PLA article) confirm the quantum “non-local” coordination between the detectors, and furthermore that this is necessary for energy to be conserved; they can also be considered as an experimental demonstration of the qubit, although obviously not of a quantum computer. In any case, they emphasize that the visible and material world is sustained by an invisible and immaterial coordination: visible and material effects require invisible causes that are not contained in space-time.

Besides the question of “non-locality”, the idea of quantum “collapse” raises two other major problems: 1) the fact that after detection the superposition disappears, and the result of the experiment is only one of the two possible ones, well defined and the same for any observer, so that in the world around us we do not see macroscopic objects like experimenters or cats in superposition states; 2) the so-called “measurement problem”: today, we still do not know precisely when and how the “collapse” occurs and the result becomes irreversibly recorded as “an elementary act of creation” (in the wording of John A. Wheeler).

The second problem I will deal with in a forthcoming essay on irreversibility. The first gives rise to the paradoxes of Schrödinger’s cat and Wigner’s friend, and I deal with it in the following.

3. “Schrödinger’s cat” and “Wigner’s friend”

Actually, “Wigner’s friend” is an improved version of the “Schrödinger’s cat”, and so I have devised a thought experiment that presents the two together:

Suppose that in our window experiment the “detector D(1)” is placed on a cat’s bell, so that, if the photon emitted by the laser source after hitting the window reaches the bell, a mechanism is triggered that kills the cat (result ‘1’ with dead cat), as Schrödinger depicted it. Bob is a friend of Eugen Wigner, a famous physicist, Nobel Prize winner in 1963, who conceived the thought experiment named after him. The window, the cat and Wigner’s friend (Bob) are all in a closed laboratory. Wigner is outside the lab and can observe what is going on inside by opening a small window. The laser source, each time it is excited, emits a single photon, which will be detected either by Bob’s detector (result ‘0’ with a live cat) or by the cat’s detector (result ‘1’ with a dead cat). As we have already said, before detection Bob considers that the photon is in a state of superposition of the two results ‘1’ and ‘0’. After detection Bob observes one result, let’s say ‘1’, and therefore sees the dead cat, and concludes that the system inside the laboratory is in the state described by |1 , cat dead⟩.

Let us now consider things from Wigner’s perspective outside the laboratory. Applying the superposition principle to the whole lab (including Bob and the cat), Wigner outside the lab, before opening the window, has to conclude that the wave function of the system consists of a superposition of the state|Bob₁ , cat dead⟩ and the state |Bob₀ , cat alive⟩ (where Bob₁ denotes “Bob observes 1”, and Bob₀ “Bob observes 0”).

In conclusion: Wigner’s friend (Bob) says that he observes the outcome “1 and the cat dead”, and at the same moment Wigner applying the superposition principle to the whole laboratory says that his friend (Bob) has 50% probability of observing “the cat alive” and 50% probability of observing “the cat dead”. In a recent version of the “Wigner’s friend” paradox, Daniela Frauchiger and Renato Renner of the Zurich Polytechnic (ETHZ) construct a more complicated thought experiment in which Wigner’s friend observes “1 and the cat dead”, and at the same moment Wigner outside the laboratory applying quantum superposition concludes that his friend observes “0 and the cat alive”.

We are thus faced with a new paradox: intuitively, that a cat is dead seems to be a fact that, when it occurs, should be valid for any observer (and for this reason Schrödinger uses this astute metaphor). However, if quantum superposition applies to observers, then, depending on the observer, the boundary between the observer and the observed system varies: Bob places himself outside the observed system, but for Wigner, Bob is part of the observed system. Thus, the domain of application of “physical laws” depends on the observer, and the experiments give different results depending on the observer: Bob can see the cat dead, while Wigner, applying quantum superposition to Bob, concludes that Bob sees the cat alive.

The paradoxes of “Schrödinger’s cat” and “Wigner’s friend” highlight the central role that the observer (the human observer in the end) plays in quantum physics in defining “physical reality” (a lesson that is often ignored): if we apply quantum superposition without restriction, then the statement that “the cat is dead” does not have an absolute and universal value, but depends on the observer; different “laws of nature” apply depending on the observer, and different observers may observe different physical realities in the same place at the same time. For example, the Sun at 2 o’clock in the afternoon may be seen by one group of observers in the astronomical coordinates corresponding to its usual orbit as described by Newton’s equations, while it may be seen by another group of observers as jumping around those coordinates.

The only way to avoid this is to introduce into our theory a postulate that prohibits the application of quantum superposition to objects of a “certain size” (we still do not know at what precise size this prohibition is activated; it is “the measurement problem,” but it is obvious that superposition does not apply to observers and cats). In other words, the fact that the visible world behaves according to regularities that allow us to predict and calculate it, and thus live comfortably in it, is due to a “mysterious” suppression of the fundamental principle of quantum physics at the “macroscopic” level. This is really shocking! We are saying that science, in order to correctly describe the ordinary visible world, where the sun and planets move according to “laws of nature” considered “inexorable”, has to introduce a violation of the principle of quantum superposition, that is, “a fundamental law of nature” after all. You have to have rocks in your head not to be surprised! (in John Bell’s wording).

But then the question arises: is there any experiment or phenomenon in which this “prohibition of superposition” is lifted, and a group of observers can see, for example, the sun dancing at 2 p.m.?

4. Fatima’s miracle of the sun

Yes! It is what happened in Cova da Iria in Fatima on October 13, 1917! In a well-documented event (see this report in the Washington Post), known as the “Miracle of the Sun of Fatima.” This “appellation” in light of quantum physics has its irony: if a miracle is understood as a “violation of the laws of nature,” certainly what the 70,000 people saw that day in Cova da Iria violates the “ordinary regularities of nature” to which we are accustomed. But what the 2 billion people in the rest of the world outside of Fatima saw—the sun following its normal orbit—also violates a “fundamental law of nature,” quantum superposition. In that sense, the “great miracle” is not what the 70,000 saw in Cova da Iria, but what 8 billion of us see every day: the sun rising at the expected place and time according to the “laws of classical physics,” and that these laws are the same in Zurich as in New York!

It can also be said that there are no “inexorable” laws of nature, but rather regularities that God arranges according to mathematical equations so that we can understand the world, develop technologies, and live comfortably—in a word, for our earthly happiness. However, nothing prevents God, if He sees fit, for example, for our eternal happiness, from “activating quantum superposition” beyond the limit: what the 70,000 saw in Fatima is as real as what the 2 billion saw in the rest of the world. The so-called “laws of nature,” latent both in miracles and in ordinary events, exist for the happiness (both earthly and eternal) of humanity: this is the only true “inexorable” law that unifies the quantum and classical realms.

I believe that Anton Zeilinger is right: we are taught by quantum physics to adopt a “mystical perspective” that reveals the “miracle” hidden in the ordinary events of each day.

(For further elaboration see this article).